3장: 모델링

모델링

빅데이터를 분석하고, 탐색을 한 후에는 예측할 수 있는 무언가가 필요하다. 기본적으로 통계를 기반으로 예측, 분석을 하지만, 머신러닝 모델 혹은 딥러닝 모델을 통하여 인공지능을 만들기도 한다.

이러한 내용을 기반으로 빅데이터 분석기사 3장에서 설명한다.

중요한 점은 별(⭐️) 로 표시해 두었다.

⭐⭐ 통계 기반 분석

• 기술 통계 분석
  • 데이터의 특성을 요약, 집계하는 것.
• t-검정
  • 두 집단 간의 평균을 비교하는 모수적 통계 방법
• anova
  • 세 개 이상의 집단 간 평균을 비교 할 때 사용하는 통게적 방법이다.

요인	제곱합	제곱평균	F
집단 간	SSR	MSR = SSR/k-1
집단 내	SSE	MSE = SSE/n-k	MSR/MSE
총	SST

• 카이제곱검정
  • 변수가 범주형일 때 사용하는 통계적 방법

⭐ 정형 데이터 마이닝

• 기술 : 의미를 단순하게 기술 (쓰는거임 암튼 쓰는거임)
• 분류 : 이미 정의된 집합으로 분류
• 추정 : 데이터에 기초해 알려지지 않은 값을 추정
• 예측 : 과거의 데이터로 미래 예측
• 연관 분석 : 데이터간 유용한 규칙을 발견
• 군집 : 데이터를 유사한 특성을 지닌 몇 개의 소그룹으로 분할

비정형 데이터 마이닝

• 텍스트 마이닝 : 대규모의 비구조적인 문서에서 의미있는 정보를 추출
• 오피니언 마이닝 : 텍스트에서 추출된 감정 등의 주관적인 정보를 정량화하는 것
• 사회연결망 분석 : 특정 네트워크의 구조나 노드 간의 관계를 분석하는 것

⭐⭐⭐ 분석 모형 유형

• 지도 학습
  • 레이블이 있는 데이터를 통해 모델을 학습시키는 방법으로, 분류와 회귀에 사용된다
• 비지도 학습
  • 레이블이 없는 데이터를 통해 모델을 학습하는 방법.
  • 군집, 차원축소, 연관규칙, 이상치탐지
• 준지도 학습
  • 레이블이 있는 데이터와 레이블이 없는 데이터를 모두 사용해 모델을 학습시키는 방법
• 강화 학습
  • 시스템이 어떤 행동을 할 때 마다 보상 및 패널티를 줘서 시스템이 받는 보상이 최대가 되는 방향으로 학습을 진행하는 방법.

분석 모형 종류

• 지도학습

  • 분류
    • 로지스틱 회귀분석, KNN, SVM, 신경망 모형, 의사결정 트리
  • 회귀
    • Lasso, Ridge, Neural Network, SVR

• 비지도학습

  • 군집
    • K-평균, DBSCAN, SOM
  • 차원축소
    • PCA, LDA, SVD, MDS
  • 연관분석
    • FP-Tree, Apiori

분석 모형 구축 절차

• 폭포수 모델
  • 장점
    • 체계적, 순차적 진행, 전체과정 이해 쉬움, 적용사례 많음, 문서 관리 용이
  • 단점
    • 고객의 요구사항 반영 빡셈, 문제 해결 및 수정 비용 큼, 피드백 반복 빡침
• 프로토타입 모델
  • 장점
    • 요구사항 이상할 때 좋음, 변경 쉬움, 요구사항 극대화 가능, 빠른 오류 발견 나이스
  • 단점
    • 만들었는데 프젝 포기하면 돈 만 아까움, 문서화하기 어려움, 변경 많으면 개발에 필요한 시간, 비용 증가
• 나선형 모델
  • 장점
    • 정확한 사용자 요구사항 파악 가능, 요구사항 변동 대처 가능, 위험 최소화, 대규모 프젝 적합
  • 단점
    • 프로젝트에 시간 많이 걸림, 반복 수행해야 됨, 위험 관리 능력 없으면 프젝 안됨

분석 도구 선정

• 엑셀
  • 다른 분석 도구보다 사용하기 쉬움, 복잡한 명령어 없이 리본 메뉴를 통해 간단하게 사용 가능
• R
  • 통계분석, 데이터 마이닝, 시각화를 목적으로 개발, 무수한 기능 확장, 즉시 사용 가능한 테스트 데이터 제공
• 파이썬
  • 다양한 플랫폼 사용 가능, 다양한 라이브러리, 다른 모듈과 연결하는 언어
• 하둡
  • 분산 환경에서 빅데이터를 처리할 수 있는 오픈 소스 프레임워크, 구축비용 저렴, 실시간 노노
• 맵리듀스
  • 대용량 데이터를 분산 병렬 컴퓨팅 통해 처리, 데이터를 key-value 쌍으로 연산
• SAS
  • 간단한 명명문만으로도 여러가지 통계분석 가능, 대용량 데이터 분석하는게 용이, 고가의 라이선스 필요, 새로운 연구 반영하기 어려움
• SPSS
  • 사회 과학 자료 분석을 위한 통계 프로그램, 고가의 라이선스, GUI있음
• Stata
  • 통계 패키지인 동시에 데이터 관리 시스템. 데이터 관리와 시각화 기능이 탁원, 라이선스가 다른 통계 프로그램보다 저렴

데이터셋 분할

• 학습 데이터셋 : 학습시킬 데이터
• 검증 데이터셋
  • 학습이 완료될 모델을 검증하기 위해 사용하는 데이터셋, 하이퍼파라미터 튜닝과 최적 모델을 선택하기 위해 사용
• 테스트 데이터셋
  • 최종 모델에 대한 성능을 평가 데이터

⭐⭐⭐ 과적합과 과소적합

• 과적합
  • 원인
    • 학습 데이터에 다양함이 없음,
    • 파라미터 과도
    • 모델이 과도하게 복잡
    • 변수의 수가 많음, 노이즈 많음
  • 해결
  • 더 많은 학습 데이터
  • 데이터 노이즈 제거
  • 모델 규제 (단순화)
  • 검증 셋을 이용 일반화 성능 향상
• 과소적합
  • 원인
    • 모델이 너무 단순
    • 규제가 너무 강함
  • 해결
    • 더 많은 파라미터
    • 모델 규제 완화
    • 다양한 비선형 모델 사용

⭐⭐⭐ 데이터 분할 방법

• 홀드아웃
  • 가장 보편적인 데이터 분할. 전체 데이터 랜덤 추출 train-test-split
• k-폴드 교차 검증
  • 전체 데이터를 중복되지 않는 K개의 데이터셋으로 나눔.
  • k-1개의 데이터셋을 학습셋으로 사용.
  • 나머지 1개를 데이터셋을 검증셋으로 함.
  • k번의 테그트를 통해 나온 모델의 성능을 평균화.
• 부트스트랩
  • 중복추출 허용. 어떤건 여러번 추출, 어떤건 아예 안 뽑힘
• startified K-폴드 교차검증
  • 불균형 데이터를 사용할때 주로 사용.
  • 각 폴드가 가지는 레이블의 분포가 유사하게 폴드를 추출

⭐⭐ 회귀분석의 가정

• 선형성
  • 독립변수가 변화 할 때 종속변수가 일정한 크기로 변화 == 선형성 만족.
  • 산점도를 통해 확인 할 수 있음.
• 독립성
  • 잔차와 독립변수의 값이 서로 독립이어야 함을 의미
• 등분산성
  • 잔차의 분산이 독립변수와 무관하게 일정.
  • 잔차가 고르게 분포.
  • 독립변수와 잔차에 대한 산점도로 확인
• 정규성
  • 잔차항이 정규분포의 형태를 띄어야 함.
  • Q-Q플롯에서 우상향 하는 직선 == 정규성 만족.
• 비상관성
  • 잔차끼리 서로 독립이면 비상관성이 있다고 판단.
  • Durbin-Watson 통계량을 통해 확인.

회귀분석의 종류

• 단순회귀분석
  • 독립변수와 종속변수가 1개씩 일 때 이 둘 사이의 인과관계를 분석하는 두 변수의 관계가 선형
• 다중회귀분석
  • 독립변수가 2개 이상 종속변수가 하나일때 사용 가능한 회귀분석으로 독립변수와 종속변수의 관계가 선형으로 표현 (단순회귀분석이 확장된 형태)
• 다항회귀분석
  • 독립 변수가 2개 이상, 종속 변수가 하나일 때 사용가능한 회귀분석.
  • 독립변수와 종속변수의 관계가 1차 함수 이상 표현
• 비선형회귀분석
  • 종속변수를 독립변수와 회귀계수의 선형적인 결합으로 표현할 수 없는 경우 사용한다.

모형 적합성

• 회귀모형의 유의성 검증
  • F-통계량을 통해 회귀모형의 통계적 유의성 확인
• 회귀계수의 유의성 검증
  • T-통계량을 통해 각 회귀계수의 유의성 확인
• 모형의 설명력
  • 결정계수(R2)를 통해 모형의 설명력 확인

⭐⭐⭐ 단순 회귀 분산분석표

요인	제곱합	자유도	제곱평균	F
회귀	SSR	1	MSR=SSR	MSR/MSE
잔차	SSE	n-2	MSE=SSE/n-2	MSR/MSE
총	SST	n-1

로지스틱 회귀분석 (오즈비)

요인 노출/발병유무	YES	NO	합계
YES	a	b	a+b
NO	c	d	c+d
합계	a+c	b+d	a+b+c+d

• 요인에 노출되었을 때 발병할 오즈 : a/b
• 요인에 노출되지 않았을 때 발병할 오즈 : c/d
• 오즈비 : ad / bc

로즈스틱 회귀분석 모형 접합도

• 회귀모형의 유의성 : 이탈도로 확인
• 회귀계수의 유의성 : wald test
• 모형의 설명력 : 의사 결정계수와 AIC 값을 통해 검증

의사결정 트리의 구성요소

• 뿌리마디
  • 학습데이터, 트리 구조가 시작되는 마디
• 자식마디
  • 하나의 마디로부터 분리되어 나간 2개 이상의 마디
• 부모마디
  • 자식 마디의 상위 마디
• 끝 마디
  • 자식 마디가 없는 마디. 각 트리의 끝에 위치하는 마디
• 중간마디
  • 끝 마디가 아닌 마디로 자식 마디가 존재하는 마디
• 가지 : 노드와 노드를 잇는 선
• 깊이 : 가지를 이루고 있는 마디의 개수

의사결정 트리 분류 기준

알고리즘	종속-이산형	종속-연속형
CHAID	카이제곱	아노바 F-통계량
CART	지니계수	분산감소량
C4.5	엔트로피지수

의사결정 트리 장단점

• 장점
  • 해석 용이
  • 이상치에 덜 민감
  • 수학적 가정이 불필요(비모수적)
  • 변수 선택 자동
  • 연속형/범주형 모두 처리
• 단점
  • 분류 기준값의 경계선 부근 자료값 == 오차가 큼.
  • 모형이 복잡하면 정확도 하락
  • 변수의 영향력 파악 힘듬
  • 새로운 자료에 불안정

인공 신경망 활성화 함수

• STEP 함수
  • 기본적인 활성 함수.
  • 계단 모양, 0 혹은 1로 표현
• Sigmoid 함수
  • 로지스틱 함수.
  • 곡선 형태, 0 혹은 1 사이 값 출력

인공 신경망 장단점

• 장점
  • 잡음에 민감하게 반응 X
  • 비선형적인 무제 분석 용이
  • 패턴 인식, 분류, 예측에 효과적
  • 스스로 가중치 학습
• 단점
  • 모형이 복잡할 경우 학습에 오랜 시간이 소요
  • 초기 가중치에 따라 전역해가 아닌 지역해로 수렴
  • 신뢰도 낮음,

하드마진 vs 소프트 마진

• 하드마진
  • 매우 엄격하게 초평면 정의
  • 모든 입력값은 초평면을 사이로 무조건 한 클래스에 속함
  • 이상치에 민감해 마진이 매우 작아질 수 있음
  • 과적합 가능성이 높음
• 소프트마진
  • 하드마진의 문제점을 해결하기 위해 여유변수를 도입
  • 오류를 어느정도 허용하여 마진을 최대로
  • 하이퍼파라미터 C를 사용
  • 마진의 크기를 최대로 하여 여유변수의 크기를 최소로 하는 결정 경계를 찾는 것이 목적

SVM 파라미터

• C
  • 오분류를 허용하는 정도.
  • C값이 작을 수록 제약이 작아 오분류에 관대하고 과소적합 가능성 큼. (vice versa)
• gamma
  • 단일 데이터 샘플이 행사하는 영향력의 정도.
  • 작을수록 과소적합의 가능성이 크다. (vice versa)

⭐⭐ SVM 장단점

• 장점
  • SVM을 이용해 결정 경계를 생성했으므로 데이터가 희소할 때 효과적.
  • 새로운 데이터가 입력됐을 때 전체 데이터포인트와의 거리를 계산하지 않고 SVM만을 계산하므로 연산량이 감소
  • 비선형 데이터도 커널트릭을 이용해 분류한다.
  • 인공신경망보다 과적합의 위험이 적다.
  • 노이즈의 영향이 적다
• 단점
  • 데이터셋의 크기가 클 수록 모델링에 많은 시간이 소요된다.
  • 확률 추정치를 반환하지 않고 블랙박스 형태라서 해석이 어려움.
  • 커널과 모델의 파라미터를 조절하기 위해 많은 테스트가 필요하다.
  • 데이터 전처리 과정이 굉장이 중요하다.

⭐⭐⭐ 연관성분석 측정지표

• 지지도
  • A와 B를 포함하는 거래의 수 (교집합) / 전체 거래의 수
• 신뢰도
  • A와 B를 모두 포함하는 거래의 수 (합집합) / A를 포함하는 거래의 수
• 향상도
  • (A와 B를 모두 포함하는 거래의 수 (합집합) X 전체 거래의 수) / (A를 포함하는 거래의 수 X B를 포함하는 거래의 수)

연관성분석 Apiori

• 1단계
  • 최소 지지도 설정
• 2단계
  • 단일 품목 중 최소 지지도 넘는 모든 품목 찾기
• 3단계
  • 2단계에서 찾은 빈발 아이템 집합만을 이용해 최소지지도를 넘는 2가지 품목 집합을 찾는다.
• 4단계
  • 위의 단계에서 찾은 빈발 아이템 집합을 이용해 최소지지도를 넘는 3가지 품목 집합을 찾는다.
• 5단계
  • 위의 단계를 반복수행해 최소지지도를 넘는 모든 빈발 아이템 집합을 찾는다.

연관성분석의 장단점

• 장점

  • 수만음 상품 간에 존재하는 유의미한 구매 패턴을 발견
  • 목적변수가 없어 특별한 분석 목적 없이도 분석 가능
  • 자료구조와 계산 과정이 간단
  • if A then B 의 형태로 간단함

• 단점

  • 품목의 수가 증가하면 계산량도 증가함
  • 거래량이 적은 품목에 대한 규칙발견이 어렵다
  • 연속형 변수를 사용하기 위해서는 몇 개의 구간으로 분할해야됨. 너무 세세하면 안됨
  • 연관성분석을 통해 발견되는 규칙의 수가 많아 유의미한 규칙 찾기 힘듬

군집 간 거리 측정 방법

• 단일연결법
  • 최단연결법
  • 각 군집에 속하는 임의의 개체 사이의 거리 중에서 가장 작은 값을 거리로 정의.
  • 가장 유사성이 큰 군집을 병합.
  • 길게 늘어진 사슬 형태의 군집
• 완전연결법
  • 최장연결법
  • 각 군집에 속하는 임의의 개체 사이의 거리 중에서 가장 큰 값을 거리로 정의.
  • 둥근 형태의 군집
• 평균연결법
  • 모든 가능한 관측치 쌍 사이의 평균 거리를 거리로 정의.
  • 가장 유사성이 큰 군집을 병합해 나가는 방법.
• 중심연결법
  • 각 군집의 중심점 사이의 거리를 거리로 정의한 방법.
  • 평균 연결법보다 계산량이 적고 모든 관측치 사이의 거리를 측정할 필요 없이 중심 사이의 거리를 한 번만 계산.
• 와드연결법
  • 군집의 평균과 각 관측치 사이의 오차제곱합의 크기를 고려한 방법.
  • 군집의 병합으로 인한 오차제곱합의 증가량이 최소가 되는 방향으로 군집을 형성.
  • 비슷한 크기의 군집끼리 병합.

군집분석 k-평균 특징

• 계층적 군집보다 계산 비용이 저렴하고 속도가 빨라 대용량 데이터를 다루는 데 적합
• 단계마다 개체가 포함된 군집이 달라질 수 있다.
• 이상치의 영향을 많이 받는다.
• 군집의 형태가 볼록한 형태가 아닌 경우 제대로 작동을 하지 않는다.

군집분석 EM 알고리즘 절차

• 모수를 임의의 값으로 설정
• E단계 : 잠재변수 Z의 기대치를 추정
• M단계 : 잠재변수 Z의 기대치를 이용해 모수의 값 추정
• 모수와 잠재변수 Z의 값이 수렴할 때 까지 E,M단계 반복

범주형 자료 분석의 종류

독립변수	종속변수	분석방법
범주형	범주형	상대적위험도, 오즈비, 카이제곱검정, 로그선형분석
범주형	연속형	T-검정, 분산분석, 다변량분산분석
연속형	범주형	판별분석, 군집분석, 로지스틱회귀분석

카이제곱 검정

• 적합도 검정
  • 일변량 분석 방법, 데이터가 어떤 이론적 분포를 따르는지 검정
• 독립성 검정
  • 변수가 2개 이상의 범주로 분할되어 있을 때 사용하는 방법.
  • 각 범주가 종속변수에 영향을 주는지 검정
• 동질성 검정
  • 각 부모 집단으로부터 추출된 관측치들이 각 범주 내에서 서로 균일한 값을 가지는지 검정.

T-검정

• 단일표본 t-검정
  • 한 집단의 평균이 모집단의 평균과 같은지?
• 대응표본 t-검정
  • 동일한 집단의 처치 전후의 차이를 알아보기 위해 사용하는 검정 방법
• 독립표복 t-검정
  • 데이터가 서로 다른 모집단에서 추출된 경우 사용하는 방법.
  • 독립된 두 집단의 평균 차이를 검정

⭐ 다변량 분석의 유형

• 다중회귀분석, 다변량분산분석, 다중로지스틱회귀분석
  • 다변량 자료가 독립변수와 종속변수로 나뉘어 있어, 독립변수를 통해 종속변수를 추정하거나 변수 간의 관계를 분석.
• 주성분분석, 요인분석
  • 변수 간의 상관관계를 이용하여 정보의 손실을 최소화하면서 변수를 요약하고자 할 때
• 군집분석, 판별분석
  • 개체들의 유사성에 기초해 개체들을 분류

요인분석의 조건

• 변수가 등간척도, 비율척도와 같은 연속형 데이터
• 관측치가 서로 독립, 각 변수는 다변량 정규분포의 형태
• 변수별로 분산이 모두 동일
• 표본의 수는 최소 50이상.

요인분석의 목적

• 여러개의 변수를 몇 개의 요인으로 묶어 자료를 요약, 변수의 차원을 축소
• 변수 내에 존재하는 상호 독립적인 특성을 발견 \
• 불필요한 변수를 제거
• 측정항목의 타당성을 검증

시계열 분석에서의 정상성 조건

• 평균이 시간에 따라 일정
• 분산이 시점에 의존하지 않음
• 공분산이 시점에 의존하지 않고 시차에만 의존

시계열 구성요소

• 추세요인 : 말그대로 추세선
• 순환요인 : 이유도 없고 주기가 일정하지 않은 변동
• 계절요인 : 일정한 주기를 가지고 상하 반복
• 불규칙요인 : 그냥 막 움직임.

⭐ 시계열 모형

• AR : 변수들의 자기상관성을 기반으로 한 시계열 모형.
• MR : 현재 데이터가 과거의 백색잡음의 선형 가중합으로 구성됨. 항상 정상성을 만족
• ARIMA : 비정상 시계열 모형. 차분이나 변환을 통해 AR, MA, ARMA 모형 등으로 정상화

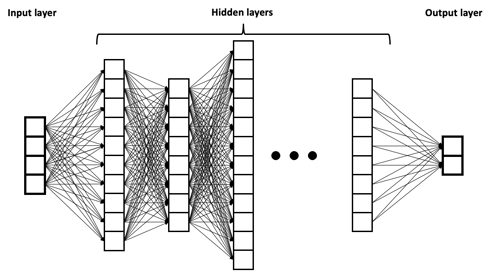
딥러닝

• 사전학습
  • RBM에 의한 사전학습을 통해 과적합 방지
• 정규화
  • 가중치가 클수록 큰 패널티를 줌. 모델의 복잡성을 줄이고 일반화 성능을 향상
• 드롭아웃
  • 일정 비율의 뉴런을 임의로 삭제.
• 배체 정규화
  • 각 층의 출력값 분포가 일정해지게 정규화
• GPU를 통한 별열처리
  • GPU병렬연산으로 시간 확 짧아짐
• 활성함수
  • RELU등의 비선형 함수를 통해 기울기 손실 문제를 해결

CNN 합성곱신경망

• 데이터의 특징을 추출, 패턴을 파악
• 합성곱층과 풀링층
• 행렬형태로 데이터를 입력, 이미지 형태 보존
• 합성곱층의 가중치에 해당
• 필터의 이동량 == 스트라이드
• 패딩은 신경망이 이미지의 외곽을 인식하게 함

RNN 순환신경망

• 순차적인 형태의 시퀀스 데이터
• 내부에 순환구조
• 모든 계층에서 같은 가중치 공유
• BPTT를 통해 가중치 학습
• 문장이 길이가 길어질 수록 장기 의존성 문제가 발생

텍스트 마이닝

• 데이터 수집
  • 코퍼스 생성
• 텍스트 전처리
  • 토큰화, 클렌징, 불용어 제거
• 피처 벡터화
  • 전처리된 데이터에서 문서별 단어의 사용 빈도를 계산, 문서 단어 행렬 생성
• 분석/시각화
  • 데이터 마이닝 기법 적용, 워드 클라우드 등을 통해 시각화

어간추출 vs 표제어 추출

• 어간추출 (stemming)
  • 정해진 규칙을 통해 접사를 제거하여 어간을 추출하는 방법.
  • 일부 철자 훼손 가능, 사전에 정의된 단어가 나오지 않을 가능성
• 표제어추출 (Lemmatization)
  • 해당 단어가 문장 속에서 어떤 품사로 쓰였는지 까지 고려하여 단어의 원형을 추출하는 방법.
  • 복잡한 과정. 느리다

사회연결망 분석 중심성 척도

• 연결 정도 중심성
  • 연결망 내에서 하나의 노드에 직접 연결된 노드의 합을 기반으로 중심성 측정
• 근접 중심성
  • 각 노드 간의 거리를 기반으로 중심성을 측정하는 방법.
  • 노드와 노드의 거리를 측정.
  • 중심성과 달리 간접적으로 거리를 측정
• 매개 중심성
  • 연결만 내에서 하나의 노드가 다른 노드들 사이에 위치하는 정도를 나타냄.
  • 한 노드가 담당하는 중재자 역할로 중심성을 측정
• 위세 중심성
  • 연결된 노드의 영향력에 가중치를 주어 중심성을 측정한다.
  • 자신의 연결 정도 중심성에서 발생하는 영향력과 연결된 노드의 영향력을 합해 위세 중심성 결정

앙상블분석

• 배깅
  • 데이터셋에서 중복 허용.
  • 랜덤 추출 (부트스트랩).
  • 각 표본을 추출하고 각 표본에 대해 예측 모델 적용
• 부스팅
  • 예측이 약한 모형들을 연결
  • 순차적으로 학습
  • 예측력이 강한 모델 생성.
  • (잘못된 데이터에 가중치 > 오류 개선)
• 랜덤 포레스트
  • 배깅의 일종.
  • 배깅에 변수 랜덤 선택(특징배깅)과정을 추가.
• 분류
  • 가장 많은 값을 최종결과. 회귀는 예측한 값의 평균
• 스태킹
  • 스태킹은 서로 다른 예측 모델을 사용해 앙상블.
  • 개별 모델이 예측한 결과값을 다시 학습 데이터셋으로 사용.

비모수통계

• 부호검정
  • 중앙값을 통해 검정하는 방법.
  • 표본의 값이 중앙값과 동일한 경우 0을 부여, 표본에서 제외
• 만-위트니 검정
  • 윌콕슨의 순위 합 검정. 독립된 두 집단의 중심 위치를 비교하기 위해 사용.
  • 정규분포에 대한 가정이 필요없어 데이터의 크기 순서만 있다면 어떤 경우에도 적용.
• 크루스칼-왈리스 검정
  • 세 개 이상 집단의 중앙값을 비교하기 위해 사용.
  • 추출된 각 표본이 중앙값만 다르고 모두 동일한 형태의 분포.
  • 일종의 순위 합 검정법.
• 런 검정
  • 각 표본이 서로 독립적이라는 가설을 검정하기 위해 사용하는 방법
  • 추출된 표본들이 어떠한 패턴 없이 무작위로 구성되었는지 검정
  • 서로 배타적인 2개의 집단으로 나누어 접근

참고자료